How Data Transmited and System Number

       First we must know bits,bytes, control and data, words also. Bits is The smallest unit quantities in data communication, only 1 or 0. Bytes is bit organized into 8. Words  Associated with computer programs and computer oprerating system than with data communication. Control and Data is control information is instruction and command  Data is representation of character  (biner, desimal etc ) or quantities.

                                                              Fig. 8 bits= 1 bytes
   
            After we know different between byte and bit , we will learn about number system in technology. Number system is number or code representing the information will give to the computer or human to understand the purpose. In the computer world we recognize four types of numbers, that says binary, octal, decimal and hexadecimal. Binary or binary digits (bits) is the number consisting of 1 and 0. Octal consisting of 0,1,2,3,4,5,6 and 7. While the decimal number consisting of 0,1,2,3,4,5,6,7,8 and 9. And hexadecimal consisting of 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E and F. Computer only understand biner and human  understand decimal, hexadecima and octal with differenfunction. All of number can converted suitable what number you want. The number are :
A.    Decimal number
 Decimal number is System number based on tens , there are 0, 1,..,9 Use a shorthand notation to indicate how many of which powers of ten are nedded. Example 123 = 1 * 10^2 + 2 * 10^1 + 3 * 10^0 . The digit 123 indicate power of 10, how many 10 making quantity of 123
B.    Binary number
Binary number is Use the number only 0 and 1. Use in data communication system and computers to control information system. The quantities indicate how many 2 represented the power. Use shorthand notation to indicate the quantities and 2 nedded
Example : 11001(binary) = 1 * 2^4 + 1 * 2^3 + 0 * 10^2+ 0 * 2^1 + 1 * 2^0 (convert decimal )
C.    Hexadecimal number
Hexadecimal is The symbols used on this system are the digits 0 through 9, plus 6 other symbol using the letters A (10) until F (15) .The number system is used to display the value of a memory address in computer programming. The quantities indicate how many 16 represented the power. Example : 10E( Hexadecimal)  =  1 * 16^2 + 0 * 16^1 + 14 * 16^0= 270(decimal)
D.    Octal number
Octal is based on number eight is composed of eight numbers are 0,1,2,3,4,5,6,7. Since it only has eight points then the sum 7 +1 = 10 (instead of 8 as well as Decimal numbers because they do not have the number 8).




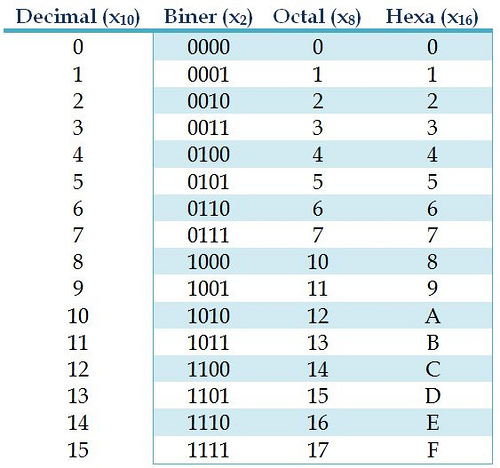
 Fig. table converted octal, decimal, hexadecimal,binary

To easy converted the number, there are several tricks and example to converted the number :
1.    Converting Binary to Octal

The conversion method is almost the same. But, because grouping by 3 bits alone, then the result is: 1010 (2) = ...... (8) Solution: Take the first three digits backward. 010 (2) = 2 (8) While the rest of the last digit, fixed-value 1. The end result is: 12.

2.    Converting Binary to Hexadecimal

The conversion method is similar to Binary to Octal. However grouping number of 4 bits. Four groups rightmost bit is the position of the unit, four second bit from the right is tens, and so on. Example: 11100011 (2) = ...... (16) Solution: group rightmost bits: 0011 = 3 groups following bits: 1110 = E results of the conversion are: E3 (16)

3.    Converting Binary to Decimal

Means or method is a little different. Example: 10110 (2) = ...... (10) is broken down into: (1x2^4) + (0x2^3) + (1x2^2) + (1x2^1) + (0x2^0) = 16 + 0 + 4 + 2 + 0 = 22 number 2 in binary multiplication is his base. While the sequential rank, signifying the rank 0 is a unit, rank 1 is tens, and so on.

4.    Octal to Binary Conversion

Actually, for the conversion of this base, it should be a little memorization is key conversion table on the top page. But can be learned easily. And take three binary only. Example: 523 (8) = ...... (2) Solution: By looking at the main table, the results obtained are: 3 = 011 2 = 010 5 = 101 Ordering number is based on the position of units, tens and hundreds. Results: 101010011 (2)

5.    Converting Hexadecimal to Binary

Methods and means almost identical with the conversion Octal to Binary. Grouping its just as much as two bits. As in the main table. Example: 2A (16) = ...... (2)

Solution:

    A = 1010,
    2 = 0010

how: A = 10

    10:2 = 5 (0) -> the rest
    5:2 = 2 (1)
    2:2 = 1 (0)
    1:2 = 0 (1)

written from the final result
results: 1010

    2:2 = 1 (0) -> the rest
    1:2 = 0 (1)

written from the final result
results: 10
so the results and writing as a record number (is parity check)->0 0| 101010 beginning unnecessary writes

6.   Converting Decimal to Hexadecimal

There are ways and methods, but for some people are still somewhat confusing. The easiest way is, first convert from decimal to binary, then convert from binary to hexadecimal. Example: 75 (10) = ...... (16) Solution: 75 divided by 16 = 4 remainder 11 (11 = B). And the conversion: 4B (16)

7.    Converting Hexadecimal to Decimal

Almost the same way as the conversion from binary to decimal. However, the base number is 16. Example: 4B (16) = ...... (10) Solution: With reference to the main table, B can be written with a value of "11". (4x16^1) + (11x16^0) = 64 + 11 = 75 (10)

8.    Converting Decimal to Octal

The trick is similar to decimal to hexadecimal conversion. Example: 25 (10) = ...... (8) Solution: 25 divided by 8 = 3 remainder 1. The result can be written: 13 (8)


9.    Converting Octal to Decimal

The method is similar to the conversion of hexadecimal to decimal. Can be followed by the example below: 764 (8) = ...... (10) Solution: (3x8^1) + (1x8^0) = 24 + 1 = 25 (10)